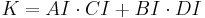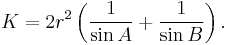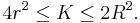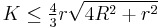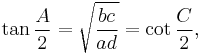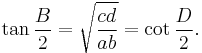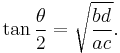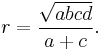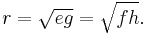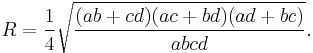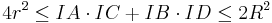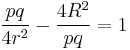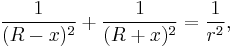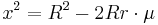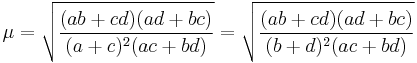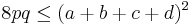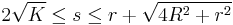Bicentric quadrilateral
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names are chord-tangent quadrilateral[1] and inscribed and circumscribed quadrilateral.
Contents |
Special cases
Examples of bicentric quadrilaterals are squares, right kites and those isosceles trapezoids where the length of the legs is the arithmetic mean of the bases.
Characterizations
A convex quadrilateral ABCD with sides a, b, c, d is bicentric if and only if opposite sides satisfy Pitot's theorem and opposite angles are supplementary, that is 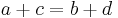 and
and 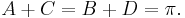
Three other characterizations concern the points where the incircle in a tangential quadrilateral is tangent to the sides. If the incircle is tangent to the sides AB, BC, CD, DA at W, X, Y, Z respectively, then a tangential quadrilateral ABCD is also cyclic if and only if any of[2]
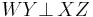 (That is, the contact quadrilateral WXYZ is an orthodiagonal quadrilateral.)
(That is, the contact quadrilateral WXYZ is an orthodiagonal quadrilateral.)
If E, F, G, H are the midpoints of WX, XY , YZ, ZW respectively, then the tangential quadrilateral ABCD is also cyclic if and only if the quadrilateral EFGH is a rectangle.[2]
According to another characterization, if I is the incenter in a tangential quadrilateral where the extensions of opposite sides intersect at J and K, then the quadrilateral is also cyclic if and only if JIK is a right angle.[2]
Yet another necessary and sufficient condition is that a tangential quadrilateral ABCD is cyclic if and only if its Newton line is perpendicular to the Newton line of its contact quadrilateral WXYZ. (The Newton line of a quadrilateral is the line defined by the midpoints of its diagonals.)[2]
Area
The area K of a bicentric quadrilateral with sides a, b, c, d is[3] [4] [5] [6] [7]
This is a special case of Brahmagupta's formula. It can also be derived directly from the trigonometric formula for the area of a tangential quadrilateral.
If a bicentric quadrilateral has tangency chords k, l and diagonals p, q, then it has the area[4]
Another formula for the area is[5]
where m and n are the bimedians of the quadrilateral.
The area can also be expressed in terms of the tangent lengths e, f, g, h as[4]
Yet another formula for the area of bicentric quadrilateral ABCD is[5]
where I is the center of the incircle. In terms of two adjacent angles and the radius r of the incircle, the area is given as[5]
If r and R are the inradius and the circumradius respectively, then the area K satisfies the inequalities[8]
There is equality (on either side) only if the quadrilateral is a square.
Another inequality for the area is
where r and R are the inradius and the circumradius respectively.[9]
Angle formulas
If a, b, c, d are the length of the sides AB, BC, CD, DA respectively in a bicentric quadrilateral ABCD, then its vertex angles are given by[5]
The angle  between the diagonals can be calculated from[6]
between the diagonals can be calculated from[6]
Inradius and circumradius
The inradius r of a bicentric quadrilateral is determined by the sides a, b, c, d according to[3]
The inradius can also be expressed in terms of the consecutive tangent lengths e, f, g, h according to[10]:p. 41
These two formulas are in fact necessary and sufficient conditions for a tangential quadrilateral with inradius r to be cyclic.
The circumradius R is given as a special case of Parameshvara's formula. It is[3]
The two radii satisfy the inequality 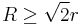 . It holds with equality only when the two circles are concentric (have the same center as each other); then the quadrilateral is a square. This inequality follows from the double inequality for the area.
. It holds with equality only when the two circles are concentric (have the same center as each other); then the quadrilateral is a square. This inequality follows from the double inequality for the area.
Another inequality concerning the two radii in a bicentric quadrilateral ABCD is
where I is the incenter.[11]
In a bicentric quadrilateral with diagonals p and q, it holds that[7]
where r and R are the inradius and the circumradius respectively.
Fuss' theorem and Carlitz' identity
Fuss' theorem gives a relation between the inradius r, the circumradius R and the distance x between the incenter I and the circumcenter O, for any bicentric quadrilateral. The relation is[1] [7] [12]
or equivalently
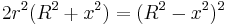 .
.
It was derived by Nicolaus Fuss (1755–1826) in 1792. Solving for x yields
Fuss's theorem says that if a quadrilateral is bicentric, then its two associated circles are related according to the above equations. In fact the converse also holds: given two circles (one within the other) with radii R and r and distance x between their centers satisfying the condition in Fuss' theorem, there exists a convex quadrilateral inscribed in one of them and tangent to the other.[13]
Applying 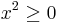 to the expression of Fuss's theorem for x in terms of r and R is another way to obtain the above-mentioned inequality
to the expression of Fuss's theorem for x in terms of r and R is another way to obtain the above-mentioned inequality 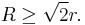
Another formula for the distance x between the centers of the incircle and the circumcircle is due to the American mathematician Leonard Carlitz (1907–1999). It states that[14]
where r and R are the inradius and the circumradius respectively, and
where a, b, c, d are the sides of the bicentric quadrilateral. Carlitz' identity is a generalization of Euler's theorem in geometry to a bicentric quadrilateral.
Other properties
- The circumcenter, the incenter, and the intersection of the diagonals in a bicentric quadrilateral are collinear.[15]
- An inequality for the product of the diagonals p, q in a bicentric quadrilateral is
-
- where a, b, c, d are the sides. This was proved by Murray Klamkin in 1967.[8]
- If two circles, one within the other, are the incircle and the circumcircle of a bicentric quadrilateral, then every point on the circumcircle is the vertex of a bicentric quadrilateral having the same incircle and circumcircle.[16] This was proved by the French mathematician Jean-Victor Poncelet (1788–1867).
- The semiperimeter s satisfies[9]
- where K is the area of the bicentric quadrilateral and r, R are the inradius and circumradius respectively.
See also
- Bicentric polygon
- Cyclic quadrilateral
- Ex-tangential quadrilateral
- Orthodiagonal quadrilateral
- Tangential quadrilateral
References
- ^ a b Dörrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solutions, New York: Dover, 1965, pp. 188–193.
- ^ a b c d Josefsson, Martin (2010), "Characterizations of Bicentric Quadrilaterals", Forum Geometricorum 10: 165–173, http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf.
- ^ a b c Weisstein, Eric, Bicentric Quadrilateral at MathWorld, [1], Accessed on 2011-08-13.
- ^ a b c Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral", Forum Geometricorum 10: 119–130, http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf.
- ^ a b c d e Josefsson, Martin (2011), "The Area of a Bicentric Quadrilateral", Forum Geometricorum 11: 155–164, http://forumgeom.fau.edu/FG2011volume11/FG201116.pdf.
- ^ a b Durell, C. V. and Robson, A., Advanced Trigonometry, Dover, 2003, pp. 28, 30.
- ^ a b c Yiu, Paul, Euclidean Geometry, [2], 1998, pp. 158-164.
- ^ a b Alsina, Claudi and Nelsen, Roger, When less is more: visualizing basic inequalities, Mathematical Association of America, 2009, pp. 64-66.
- ^ a b Inequalities proposed in “Crux Mathematicorum”, 2007, Problem 1203, p. 39, [3]
- ^ M. Radic, Z. Kaliman, and V. Kadum, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) 33–52.
- ^ Post at Art of Problem Solving, 2009, [4]
- ^ Salazar, Juan Carlos (2006), "Fuss's Theorem", Mathematical Gazette 90 (July): 306–307.
- ^ Byerly, W. E. (1909), "The In- and-Circumscribed Quadrilateral", The Annals of Mathematics 10: 123–128.
- ^ Calin, Ovidiu, Euclidean and Non-Euclidean Geometry a metric approach, [5], pp. 153–158.
- ^ Bogomolny, Alex, Collinearity in Bicentric Quadrilaterals [6], 2004.
- ^ Weisstein, Eric W. "Poncelet Transverse." From MathWorld--A Wolfram Web Resource, [7]
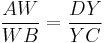
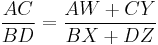
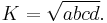
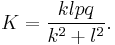
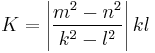
![K=\sqrt[4]{efgh}(e%2Bf%2Bg%2Bh).](/2012-wikipedia_en_all_nopic_01_2012/I/6c1818188faa0e5a7812cbe210ae4e32.png)